Have you ever wondered how Amazon suggets to us items to buy when we’re looking at a product (labeled as “Frequently bought together”)?
For example, when checking a GPU product (e.g. GTX 1080), amazon will tell you that the gpu, i7 cpu and RAM are frequently bought together.
Which is true because a lot of people buy their components grouped when building a desktop pc.
I always thought of it as a block box that takes a specific product (or specifications of that product, like its category) and outputs a list of related products. Not until I recently started studying Data Mining and came across Association Rule Mining/Learning.
Association Rule Mining
Given a set of transactions, association rule mining is simply the process of finding relations between a set of items such as an occurence of one (or many) results in the occurence of another (or many).
An association rule is often represented as $X \rightarrow Y$ where $X$ and $Y$ are itemsets.
A popular example used to explain association rules is the store expample.
In a store, a lot of people come and buy products everyday.
We can look at the list of products bought in a period, see what products are bought together and create our rules.
We can then use these rules to help us make decisions, e.g. put certain products together, add collective discounts.
Of course it’s not as easy as picking whatever products that come together.
Not only the generation of such rules takes time, but the rules also have to reflect on frequent products and not random products bought together.
Vocabulary
- Itemset: A list of one or more items (products in our example).
- Support count $\sigma$: The number of times an itemset occurs.
- Support: The fraction of transactions that contain an itemset.
- Frequent itemset: An itemset that whose support is above or equal to a threshold (called minimum support).
- Support of an association rule: The fraction of transactions that contain both $X$ and $Y$.
- Confidence of an association rule: How often items in $Y$ appear in transactions that contain $X$.
Apriori Algorithm
Association rules are great and everything, but how do we generate them?
The easiest answer that comes to mind is to bruteforce all possible rules. This is VERY inefficent because we’ll have to compute the support and confidence of all these rules, which is computationally infeasable in medium to large datasets.
A more “sophisticated” way to generate the rules is to use the Apriori algorithm.
The apriori algorithm reduces the number of candidates thanks to the following principle:
If an itemset is frequent, ALL of its subsets are frequent.
We can think of this backwards, every unfrequent itemset cannot be used to generate a frequent itemset.
In case you’re wondering, here’s why the Apriori principle holds:
$$
\forall X, Y : (X \subseteq Y) \longrightarrow s(X) \geq s(Y)
$$
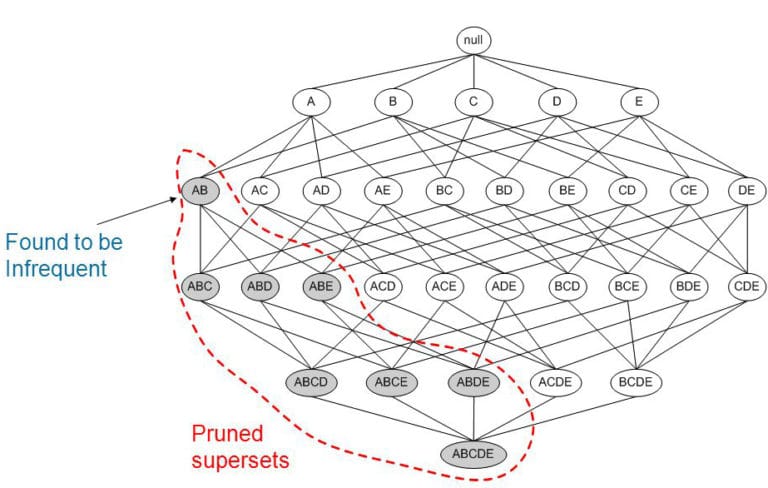
Illustrating Apriori Principle
Steps of the algorithm:
- Extract all the frequent 1-itemsets (unique items in all the transactions).
- Create new candidates (itemsets) using the previous frequent itemsets.
- Calculate their supports and eliminate unfrequent ones.
- Repeat 2 and 3 until we don’t have any more candidates.
- Extract all the association rules from all the frequent itemsets and eliminate those who have low confidence.
Example
Let’s take for example the following list of transactions:
| TID | Items |
|---|---|
| 1 | Apple, Orange, Lime |
| 2 | Orange, Lime, Strawberries, Banana |
| 3 | Blueberries, Lime, Banana, Orange |
| 4 | Grapes, Orange, Banana |
| 5 | Apple, Blueberries, Raspberries, Banana |
| 6 | Orange, Apple, Banana |
| 7 | Lime, Orange, Apple, Banana |
| 8 | Avocado, Strawberries, Orange |
| 9 | Orange, Lime, Banana |
| 10 | Apple, Banana, Orange, Lime |
In this example, our minimum support is 0.5 and our minimum confidence 0.5.
Let’s extract the 1-itemsets from it and calculate their support:
| Itemsets | Support |
|---|---|
| Apple | 0.5 |
| Orange | 0.9 |
| Lime | 0.6 |
| Strawberries | 0.2 |
| Blueberries | 0.2 |
| Banana | 0.8 |
| Raspberries | 0.1 |
| Grapes | 0.1 |
| Avocado | 0.1 |
As you can see, a lot of itemsets were removed because they don’t meet the minimum support threshold.
Now let’s extract the 2-itemsets using the 1-itemsets and calculate their support:
| Itemsets | Support |
|---|---|
| Apple, Orange | 0.4 |
| Apple, Banana | 0.4 |
| Apple, Lime | 0.3 |
| Orange, Banana | 0.7 |
| Orange, Lime | 0.6 |
| Banana, Lime | 0.5 |
We have less elements to consider at each step, which reduces the number of supports we need to calculate.
Now to our 3-itemsets:
| Itemsets | Support |
|---|---|
| Banana, Orange, Lime | 0.5 |
Finally, we’re left with one 3-itemset that happens to be frequent.
Thanks to the Apriori algorithm, we ended up checking 16 candidate itemsets instead of many more.
The next and last step is creating the association rules from all the frequent itemsets that have at least 2 items and calculate their confidence.
| X | Y | Support of X | Support of X+Y | Confidence |
|---|---|---|---|---|
| Orange | Banana | 0.9 | 0.7 | 0.77 |
| Orange | Lime | 0.9 | 0.6 | 0.66 |
| Banana | Lime | 0.8 | 0.5 | 0.62 |
| Banana | Orange, Lime | 0.8 | 0.5 | 0.62 |
| Orange | Banana, Lime | 0.9 | 0.5 | 0.55 |
| Lime | Banana, Orange | 0.6 | 0.5 | 0.83 |
| Banana, Orange | Lime | 0.7 | 0.5 | 0.71 |
| Orange, Lime | Banana | 0.6 | 0.5 | 0.83 |
| Banana, Lime | Orange | 0.5 | 0.5 | 1 |
Luckily, all our association rules met our minimum confidence threshold!
If you noticed, we got an association rule with a confidence equal to 1. This means that WHENEVER we see its X, the Y will be there in the transactions.
If we check to make sure, all the transactions containing a Banana and a Lime contain indeed an Orange.
Conclusion
As you can see, association rule minig is very important. It helps us incover relations between items and can help us make better decisions overall.
If you’re interested to see the implementation of the apriori algorithm, here’s mine in github.